Quantum-computing-enhanced algorithm unveils potential KRAS inhibitors

Benchmark setup

Our benchmark used both classical and quantum hardware. Our classical computational setup was based on a cluster equipped with graphics processing unit (GPU) nodes. This cluster consisted of two GPU nodes, each with specific features. These features included two AMD EPYC 7V13 64-core processors, resulting in a total of 128 central processing unit cores per node. In addition, each node was equipped with 512 GB of random-access memory (RAM). The nodes also contain eight AMD Instinct MI100 GPUs, each with a GPU RAM of 32 GB. For the classical training, we used four of these GPUs in parallel (that is, one GPU node). Furthermore, we used an Nvidia GPU (RTX3090Ti) to facilitate our classical–quantum simulations. For the quantum hardware setup, we used the Guadalupe quantum system, equipped with 16 qubits and a Falcon r4P processor type. Our QCBM model, accompanied by an error correction circuit, was executed on this quantum processor.

Regarding software, we used several packages provided by Zapata AI under the Qml core agreements. We implemented our variational quantum circuit and classical LSTM model using the Qml Core Python package. We used the STONED–SELFIES and VirtualFlow 2.0 packages to prepare a diverse dataset. Additionally, we used RDkit and Insilico APIs to compute the reward value and conduct some postprocessing analyses. The QCBM model underwent a training regimen spanning 30 epochs. In contrast, the LSTM model was trained over a total of 40 epochs.

We used the Optuna platform to optimize the hyperparameters in the benchmarking. We ran Optuna tuning for 100 trials for each model to determine the optimal number of QCBM layers, number of LSTM layers and embedding dimensions. Additionally, we tuned the sampling temperature, which defines the balance between determinism and stochasticity in the model, particularly between the prior input and the LSTM output.

Computational benchmarks: classical versus quantum models

Tartarus benchmark

We used the Tartarus platform²⁶ to benchmark our proposed QCBM–LSTM methodology against an array of classical state-of-the-art models, including REINVENT³⁷, SMILES–VAE³⁸, SELFIES–VAE³⁹, MoFlow⁴⁰, SMILES–LSTM–HC^41,42, SELFIES–LSTM–HC, GB–GA⁴³ and JANUS⁴⁴. The study focused on three protein targets selected from the Tartarus dataset: (1) PDB 1SYH, an ionotropic glutamate receptor associated with neurological and psychiatric disorders such as Alzheimer disease, Parkinson disease and epilepsy⁴⁵; (2) PDB 6Y2F, the main protease of severe acute respiratory syndrome coronavirus 2, crucial for its RNA translation⁴⁶; and (3) PDB 4LDE, the β₂-adrenoceptor G-protein-coupled receptor, a cell-membrane-spanning receptor that binds to adrenaline, a hormone implicated in muscle relaxation and bronchodilation⁴⁷. For each target, we had a dual objective: to generate novel molecules that exhibit strong binding affinity to the specified proteins, as determined by active sites assigned by Tartarus, and to minimize the docking score using QuickVina 2 (ref. ⁴⁸). Additionally, these molecules were required to pass a comprehensive set of filters designed to eliminate reactive, unsynthesizable or unstable groups, thereby streamlining the drug discovery process. The top-performing molecules, after filtering, were subjected to a refined rescoring using a more precise scoring function provided by SMINA⁴⁹, at an increased level of exhaustiveness.

We conducted experiments using the QCBM with 16 qubits as a quantum prior and the LSTM as a classical model. The local filter from the Tartarus paper served as the reward function to train the QCBM. As recommended by Tartarus, our models were trained on a subset of 150,000 molecules from the Developmental Therapeutics Program open compound collection^50,51, referred to as DATASET in Supplementary Table 1. Notably, all 150,000 structures underwent a rigorous screening process using structural filters to eliminate reactive, unsynthesizable or unstable groups. As such, generative models adept at capturing the distribution of the provided molecule set would exhibit a correspondingly high success rate in generating novel molecules without structural violations. Our observations indicated that only a few generative models demonstrated a high success rate. However, the QCBM–LSTM model was very strong in producing a substantial number of high-quality samples that successfully meet the filter criteria, as evidenced by the elevated success rate depicted in Supplementary Table 1. Consequently, we believe that the incorporation of a quantum prior leads to improved distribution matching. We further benchmark the influence of a classical–quantum prior in the subsequent section. Moreover, our analysis revealed that, for the PDB 4LDE target, our model generated the highest-scoring molecules relative to other generative models. While the docking scores for the remaining two targets were not as high as those produced by classical algorithms, we speculate that incorporating a docking-score-based reward, in conjunction with the filter success rate, could potentially improve our results.

Benchmarking of prior distributions

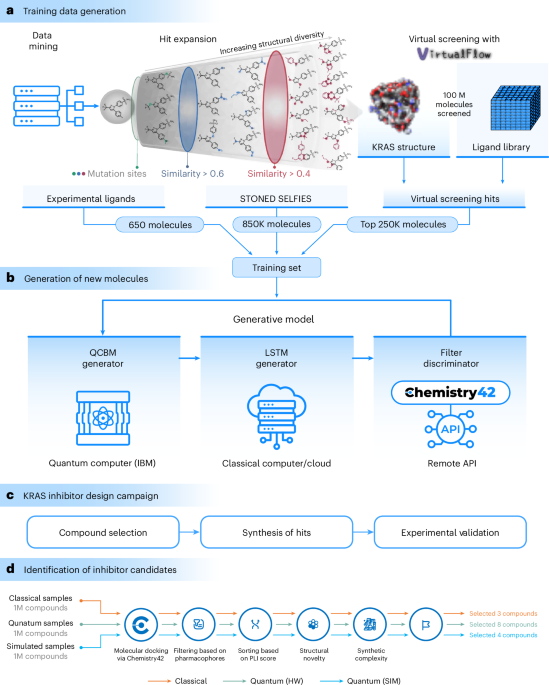
To evaluate the impact of prior selection on the quality of the molecules generated by our model, we trained four distinct model variants, each incorporating different priors (Extended Data Fig. 1b). Specifically, we examined a QCBM prior and implemented it on both a quantum simulator and a hardware backend, in contrast with an MQCBM operating exclusively on a quantum simulator and a classical LSTM model devoid of quantum priors. These models were tasked with designing KRAS inhibitors, using a meticulously curated dataset of over 1 million molecules (Fig. 1). Extended Data Figure 1b showcases the optimal results obtained following a comprehensive optimization of the corresponding architectures using Optuna⁵². We assessed the quality of the generated molecules using two distinct sets of criteria: one derived from Tartarus²⁶, termed the ‘local filter’, and a more stringent set provided by Chemistry42, termed the ‘Chemistry42 filter’. In both assessments, we observed that incorporating a quantum prior enhanced the success rate, as gauged by the proportion of molecules satisfying the criteria set by the two filters. Furthermore, using the top model from each prior category, we sampled 5,000 molecules that successfully met the filter criteria and examined their respective docking scores (Supplementary Table 2). Intriguingly, these molecules displayed comparably high docking scores as determined by QuickVina 2 and the PLI score, as evaluated by Chemistry42. Additionally, the synthesized molecules demonstrated consistent metrics across various parameters, including the diversity fraction, uniqueness fraction, Chemistry42 reward and Chemistry42 synthetic accessibility score²⁵.

Encouraged by our observation that quantum priors enhance molecule quality, we further investigated the influence of the number of qubits used in modeling priors on the quality of generated molecules (Extended Data Fig. 1d). Specifically, we analyzed the percentage of 5,000 uniquely generated random molecules that satisfied a series of local filters. Interestingly, our findings revealed that the success rate correlated roughly linearly with the number of qubits used in modeling the prior, indicating a direct relationship between the complexity of the quantum model and the effectiveness in generating high-quality molecules. This trend underscores the potential of increasing qubit numbers in quantum models to improve molecular design outcomes systematically.

SPR conditions

A Biacore 8K system was used for all experiments. For preliminary compound screening, N-terminal biotinylated KRAS-G12D protein (synthesized by VIVA Biotech; purity ≥ 95%) was captured on a sensor chip SA (GE Healthcare) at a density of about 2,000 RU. Protein immobilization was conducted using 1× HBS-EP+, 2 mM TCEP and 2% DMSO as a running buffer. Protein was injected for 70 s at a flow rate of 5 μl min⁻¹. The protein concentration was 5 μg ml⁻¹. We performed an initial screening of compounds prepared samples by serial twofold dilutions from 200 μM to 0.39 μM in 1× HBS-EP+, 2 mM TCEP and 2% DMSO. Samples were injected for 60 s at a flow rate of 30 μl min⁻¹ and dissociation time of 180 s. A Biacore 8K machine was used to carry out the SPR experiments and subsequent data analysis.

MaMTH-DS dose–response assays

MaMTH-DS FLP HEK293 reporter cell lines²⁸ stably expressing KRAS (WT or mutant), HRAS, NRAS or artificial membrane-anchored ALFA tag bait alongside Raf1 (for Ras baits) or nanobody ALFA (for artificial bait) preys were seeded into 384-well white-walled, flat-bottomed, tissue-culture-treated microplates (Greiner, 781098) at a concentration of 100,000 cells per ml (50 μl total volume per well) in DMEM, 10% FBS and 1% penicillin–streptomycin. Seeding was performed using a MultiFlo-FX multimode liquid dispenser (BioTek). Plates were left at room temperature for 30–60 min following seeding before transfer to a Heracell 150i incubator (Thermo Fisher Scientific) and growth at 37 °C in 5% CO₂ for 3 h. After growth, 10 μl of DMEM, 10% FBS and 1% penicillin–streptomycin supplemented with 3 μg ml⁻¹ tetracycline (to induce bait and prey expression; BioShop, TET701) and 60 ng ml⁻¹ epidermal growth factor (to stimulate Ras signaling; Sigma, E9644) was added to each well using a multichannel pipette. As appropriate, a 6× concentration of drug (or DMSO only) was also included in the medium, with all lower concentrations produced by serial dilution starting from the highest concentration solution. Plates were then grown overnight (18–20 h) at 37 °C in 5% CO₂. A luciferase assay was performed the next day using 10 μl of 20 μM native coelenterazine substrate (Nanolight, 303) per well. Luminescence was measured using a Clariostar plate reader (BMG Labtech) with a gain of 3,200–3,800 and a 1-s integration time. All data analysis was performed using Microsoft Excel and GraphPad Prism. Curve fits were performed in Prism (nonlinear regression) using log(inhibitor) versus response curves, with a variable slope (four parameters) bottom-constrained to zero.

Cell viability assay

MaMTH-DS FLP HEK293 reporter cell lines²⁸ stably expressing KRAS (WT or G12V mutant) bait alongside Raf1 prey were seeded into 96-well white-walled, μCLEAR flat-bottomed, tissue-culture-treated plates (Greiner, 655098) at 40,000 cells per well in DMEM, 10% FBS and 1% penicillin–streptomycin (60 μl total volume per well). Seeding was performed using a MultiFlo-FX multimode liquid dispenser (BioTek). Plates were left at room temperature for 30–60 min following seeding before transfer to a Heracell 150i incubator (Thermo Fisher Scientific) and growth at 37 °C in 5% CO₂ for 3 h. After growth, 30 μl of a 3× concentration of the drug (or DMSO only) in DMEM, 10% FBS and 1% penicillin–streptomycin was added to wells, with all lower concentrations produced by serial dilution starting from the highest concentration solution (final drug concentration: 30 μM to 123 nM). Plates were then grown overnight (18–20 h) at 37 °C in 5% CO₂. The effect of the drug on cell viability was assessed by the CellTiter-Glo luminescent cell viability assay from Promega (G7570). Briefly, 90 μl of the CellTiter-Glo reagent was added directly into each well following 30-min equilibration of the plate at room temperature. Contents of the wells were mixed on an orbital shaker for 2 min and plates were then incubated at room temperature for 10 min to stabilize the luminescence signal. Luminescence was measured using a Clariostar plate reader (BMG Labtech) with a gain of 3,600 and a 1-s integration time. Values represent the mean ± s.d. of three replicates for each tested drug concentration. All data analysis was performed using Microsoft Excel and GraphPad Prism.

Protein purification and NMR: sample preparation

A construct encoding N-His–TEV (tobacco etch virus)–KRAS-G12D was transformed into BL21(DE3) cells. The cells were grown in minimal medium containing 1 g l⁻¹ [¹⁵N]H₄Cl and 4 g l⁻¹ glucose to an optical density at 600 nm of ~0.7–1.0 and induced with 1 mM IPTG for 16 h at 16 °C. Cells were pelleted and resuspended in lysis buffer (20 mM sodium phosphate pH 8.0, 500 mM NaCl, 10 mM imidazole, 1 mM 2-mercaptoethanol and 5% (v/v) glycerol) containing PMSF and benzamidine. Protein was purified over a His trap column (Cytiva) following standard Ni-affinity protocols (wash with 10 mM and 20 mM imidazole and then elute with 300 mM imidazole) and the His-tag was removed by TEV cleavage. KRAS-G12D was further purified by size-exclusion chromatography using a Superdex 75 Increase column (10/300 GL) with PBS buffer (137 mM NaCl, 2.7 mM KCl, 10 mM Na₂HPO₄ and 2 mM KH₂PO₄, pH 7.4) containing 10 mM EDTA. The samples were prepared by mixing 30 μM of protein with 200 μM ISM018-2 in the presence of 2% DMSO-d₆, 5 mM GDP and 15 mM MgCl₂ in the buffer. The purification protocols were adapted from previously published protocols for KRAS-G12C (ref. ⁵³) and KRAS-G12D (ref. ⁵⁴).

NMR experiments and analysis

¹H–¹⁵N TROSY HSQC experiments were recorded at 298 K on an 800-MHz Bruker spectrometer equipped with an AVANCE III console and a cryogenically cooled probe. The acquired spectra were processed using NMRPipe⁵⁵ and were analyzed using ccpnmr 2.0 (ref. ⁵⁶). The chemical shifts were transferred from Biological Magnetic Resonance Bank 27719 (ref. ⁵⁴). The CSPs on both ¹H and ¹⁵N dimensions were used to calculate the weighted CSP⁵⁷ and these values were then plotted onto the PDB structure using PyMol to map the regions that took part in ligand binding or underwent conformational changes upon ligand binding.

Experimental validation methods

Chemistry42 methods: after screening and selection of promising candidate structures for synthesis

Our selection process relied on a tiered system of the following criteria:

• Structural and compositional parameter filters, such as hydrogen bond donor count and aromatic atom fraction.

• Property evaluation for molecular weight, lipophilicity and other physicochemical traits.

• Medicinal chemistry filters to exclude problematic structural motifs.

• A synthetic accessibility assessment based on the ReRSA model⁵⁸.

• Three-dimensional pharmacophoric analysis in reference to an X-ray cocrystal structure (PDB 7EW9) (Extended Data Fig. 4).

• PLI scoring to estimate binding efficiency.

• An overall reward calculation integrating the above scores

For synthesis candidacy, we applied more demanding conditions, ensuring compounds met the following enhanced benchmarks:

• Clearance of all Chemistry42 filters.

• An aggregate reward value exceeding 0.7.

• A PLI score indicative of strong KRAS binding (<−8 kcal mol⁻¹).

• A pharmacophore match score above 0.7.

• Favorable synthetic accessibility with a ReRSA score under 5.

After screening, molecules were clustered and ranked within clusters by chemical similarity, allowing for expert analysis to further prioritize on the basis of novelty and structural intricacy, culminating in a selection of 100–150 molecules for potential synthesis and subsequent examination.

Experimental evaluation methods of generated compounds

From the pool of identified structures, we synthesized and characterized 15 compounds. Detailed methodologies of this process are elaborated in the Supplementary Information. The molecular structures of the two most promising compounds (ISM061-018-2 and ISM061-022) are showcased in Fig. 2a,e. Each synthesized compound underwent a rigorous two-phase evaluation; their binding affinities were determined using SPR and their biological efficacies were gauged through cell-based assays. Notably, compound ISM061-018-2, engineered through our hybrid quantum model (Supplementary Table 3), demonstrated a substantial binding affinity to KRAS-G12D, registered at 1.4 μM. To delve deeper into this molecule’s effectiveness across a spectrum of KRAS mutants, we commenced an extensive series of tests using a cell-based assay. Specifically, we evaluated the molecule’s performance in a biological context using a commercial cell viability assay (CellTiter-Glo, Promega) in conjunction with MaMTH-DS, an advanced split-ubiquitin-based platform for the real-time detection of small molecules targeting specific cellular interactions^{28,29,30,31,32,33,34}.

Furthermore, the biological activity of ISM061-018-2 was rigorously tested. Importantly, it demonstrated no detrimental impact on the viability of HEK293 cells, even when expressing either KRAS WT or KRAS-G12V bait in MaMTH-DS format and being subjected to concentrations as high as 30 μM for 18–20 h, showing that the compound did not possess any general, nonspecific toxicity (Fig. 2d). Subsequent testing using MaMTH-DS across a spectrum of cell lines expressing various KRAS baits (WT and five clinically important oncogenic mutants) in combination with Raf1 prey (a recognized KRAS effector) revealed a dose-responsive inhibition of interactions, with IC₅₀ values in the micromolar range (Supplementary Table 3). The compound’s activity was not specific to mutants, as it targeted both WT and mutant interactions with similar efficacy. It also showed comparable effectiveness in disrupting the interactions of WT NRAS and HRAS baits with Raf1 prey (Fig. 2c). However, it had no effect on the interaction of a completely unrelated artificial bait–prey control pair (consisting of membrane-anchored ALFA tag bait and nanobody ALFA prey)³⁶, supporting the biological specificity of the interaction (Fig. 2c). Collectively, these results support a potential pan-Ras activity of ISM061-018-2.

ISM061-022 (Fig. 2e) also stood out as a compound of promise, particularly because of its selectivity toward certain KRAS mutants. Within our in vitro examination, ISM061-022 demonstrated a concentration-dependent inhibition of KRAS interactions (Fig. 2f), while manifesting only a mild, general impact on cell viability at higher concentrations over an 18–20-h exposure (Fig. 2g). The observed inhibition mirrored that of ISM061-018-2 yet displayed enhanced selectivity toward certain KRAS mutants, particularly KRAS-G12R and KRAS-Q61H, which were most receptive to the compound’s action (Fig. 2f and Supplementary Table 4). Diverging from ISM061-018-2, ISM061-022 did not show binding to KRAS-G12D. The compound also demonstrated activity against WT HRAS and NRAS, although it was less potent against HRAS. Notably, the compound had an unusual effect on our artificial control interaction pair, leading to a distinct dip to approximately 50% residual activity at concentrations of 250–500 nM, before climbing again and ultimately leading to mild enhancement of the interaction at higher micromolar concentrations (Fig. 2f). This distinct pattern suggests an alternative mode of action for ISM061-022, revealing at least some degree of nonspecific activity, although partial specificity for mutant KRAS protein does still appear to be in evidence. Further investigation into the mechanism of action of this molecule will be the focus of future study.

In essence, these live-cell experimental observations underscore the robustness of our approach, effectively identifying small-molecule candidates with biological activity. This underlines the potential of our methodology to address and surmount the complexities inherent in targeting clinically challenging biomolecules.

This section explains the methods and workflow incorporated in our proposed approach, offering a comprehensive understanding of the mechanisms used in our study. Figure 1 illustrates the workflow we used in our study.

Data acquisition and preprocessing

Our preliminary dataset, sourced from Insilico Medicine, included approximately 650 data points. These were selectively collated from existing literature, specifically targeting the KRAS-G12D mutant (Fig. 1). Given the dataset’s limited size, we opted to expand it to improve the robustness of our model during training.

STONED–SELFIES

We used the STONED–SELFIES²⁴ algorithm (https://github.com/aspuru-guzik-group/stoned-selfies) to mine our initial set of 650 molecules. For a given molecule in SMILES format, we first randomized the string using RDKit. These randomized strings were then converted into SELFIES. Each SELFIES string underwent mutations (in the form of character deletions, replacements and additions) up to 500 times. Subsequently, the synthesizability and stability of the mutated strings were assessed using Chemistry42. We generated 850,000 molecules, which served as the training set for our generative models.

Virtual screening process

VirtualFlow 2.0 (ref. ²³) was used to identify additional molecules predicted to bind to KRAS-G12D. The adaptive target-guided (ATG) method performed the virtual screening in two stages. In the first stage, the ATG prescreen was performed, in which a spare version of the 69 billion REAL space from Enamine (version 2022q12) was screened. In the second stage, the most potent tranches of ligands were screened in full, amounting to 100 million ligands. The docking program used was QuickVina 2 (ref. ⁴⁸), with exhaustiveness set to 1 in both stages of the screen. The screen was carried out in the Amazon Web Services cloud computing platform. The protein structure used in the screen was PDB 5US4 (ref. ⁵⁹), which was prepared before the virtual screen with Schrödinger’s protein preparation wizard (addition of hydrogens and protonation state prediction). The size of the docking box was 14 × 14 × 20 ų.

Quantum-assisted algorithm

As shown in Fig. 1, our quantum-assisted model was a hybrid algorithm composed of both quantum and classical generative components. The quantum generative model used a QCBM model while the classical component used an LSTM model. Extended Data Fig. 3 illustrates the flowchart of our proposed generative model.

Within this model, we used Chemistry42 and a local filter to validate sample generation at each step, which was then used to train the QCBM model. The QCBM model, a quantum circuit model, was executed on a quantum processing unit. Subsequently, samples from the trained QCBM were fed into the LSTM model, which generated sequences on the basis of these samples. The reward value for each sample was computed at every step using the local filter until epoch 20, after which we selected Chemistry42. This reward value was then used to train our quantum generative model. During the first epoch, no rewards were available; hence, the algorithm sampled from the untrained QCBM model, designated as X_i. From the second epoch onward, rewards were computed, allowing us to calculate the softmax of the rewards for each X_i, where i ∈ [1, N]. The corresponding pseudocode can be found in Algorithm 1.

Quantum-computing-enhanced workflow

Our methodology encompassed a comprehensive workflow, extending from data preparation to experimental validation, as delineated in Fig. 1. This workflow was structured into three pivotal stages:

(1) Generation of training data. We initiated the process by constructing a robust dataset for training our generative model to target the KRAS protein. The foundation of this dataset was approximately 650 experimentally confirmed KRAS inhibitors, compiled through an extensive literature review^60,61,62,63. Acknowledging the necessity of a more expansive dataset to develop a model for ligand design effectively, we adopted a two-pronged approach: virtual screening and local chemical space exploration. In the virtual screening phase, we used VirtualFlow 2.0 (ref. ²³) to screen 100 million molecules, applying Enamine’s REAL library⁶⁴ in conjunction with molecular docking techniques. The top 250,000 compounds from this screen, exhibiting the lowest docking scores, were subsequently integrated into our dataset. Complementing this, the local chemical space exploration was conducted using the STONED–SELFIES algorithm²⁴, which was applied to the 650 experimentally derived hits. This algorithm distinctively introduces random point substitutions into the SELFIES representations^39,65,66 of the molecules, thereby generating novel compounds that maintain a structural resemblance to the starting point. The resulting derivatives were filtered on the basis of synthesizability, culminating in the addition of 850,000 molecules to our training set.

(2) Generation of new molecules. Our approach was structured around the integration of three primary components: (1) the QCBM; (2) the classical LSTM model; and (3) Chemistry42 for artificial-intelligence-driven validation, as shown in Extended Data Fig. 3. The QCBM generator¹⁶ used a 16-qubit IBM quantum processor with quantum circuits to model complex data distributions. The integration method of quantum priors into the LSTM architecture (Supplementary Fig. 4) involved merging molecular information encoded in SELFIES and quantum data by addition or concatenation to form samples, \({X}^{{\prime} }

Algorithm 1

Algorithm 1 provides an overview of quantum-assisted drug discovery using an LSTM framework. This pseudocode details the iterative process, starting with the initialization of the LSTM and QCBM models, followed by the generation and validation of new compounds. Valid compounds are subjected to a reward calculation and probability assessment, which in turn inform the subsequent training of the QCBM (Algorithm 2). This cycle continues until convergence, illustrating the dynamic interplay between quantum predictions and LSTM-generated compounds underpinned by the Chemistry42 evaluation.

1: Initialize: LSTM, QCBM, filter (Chemistry42)

2: Generate initial samples X_i from QCBM

3: while not converged do

4:  Train LSTM with X_i

5:  LSTM generates a new compound from the current samples X_i

6:  Validate the new compound with the filter

7:  if new compound is valid then

8:    Compute rewards for the new compound

9:    Compute probabilities P(X_i) for each new compound

10:    Train QCBM with X_i and P(X_i)

11:    Generate new X_i from QCBM

12:  end if

13: end while

QCBM model

The QCBM model represents a quantum variational generative model, necessitating a classical optimizer to train its parameters. The total count of these parameters was computed with the number of qubits and layers defined in the model (Extended Data Fig. 5). Upon specifying the parameters, denoted as θ_n, we obtain a quantum state \(\left\vert \psi (\theta )\right\rangle\). Here, each θ_n exerts an impact on the wave function, expressed as ψ(θ). To optimize these parameters θ, the model is initially configured with randomly assigned parameters \(\left\vert \psi (\theta )\right\rangle\). These parameters are subsequently calculated throughout the training process. The training of the QCBM model involves minimizing the exact negative log-likelihood (exact NLL) loss function.

Classical model: LSTM model

LSTM networks (Fig. 1) were used for the classical part of this architecture. LSTM is simple and has a good record of learning the string pattern in natural language processing for a long time. LSTM networks are specialized recurrent neural networks capable of learning long-term dependencies in sequence data⁶⁷. They are particularly useful in applications where the context from earlier parts of the sequence is needed to interpret later parts, such as in natural language processing and time-series forecasting⁶⁸. The LSTM architecture consists of a chain of repeating modules called cells. Each cell contains three gates that control the flow of information:

1. 1.

   Forget gate: This gate decides what information from the cell state should be thrown away or kept. It takes the output of the previous LSTM cell and the current input and passes them through a sigmoid function, outputting a number between 0 and 1 for each number in the cell state, where 0 means ‘completely forget this’ and 1 means ‘completely keep this’.

2. 2.

   Input gate: This gate updates the cell state with new information. It has two parts: a sigmoid layer called the input gate layer and a hyperbolic tangent layer. The sigmoid layer decides what values to update and the hyperbolic tangent layer creates a vector of new candidate values that could be added to the state.

3. 3.

   Output gate: This gate decides the next hidden state. The hidden state contains information on previous inputs. The hidden state is used to calculate the output of the LSTM and the next hidden state.

The following equations can describe the LSTM’s operations:

Here, σ is the sigmoid activation function, W and b are the weight matrices and bias vectors for each gate and x_t is the input at time t⁶⁹.

Training an LSTM involves optimizing the network’s weights and biases to minimize a specific loss function. This is typically accomplished using gradient-based optimization algorithms such as stochastic gradient descent or Adam⁷⁰. The backpropagation through time algorithm was used to compute the gradients relative to the loss function, considering the sequential nature of the data⁷¹. The networks were trained using the Adam optimizer with the NLL loss function; to mitigate overfitting, regularization techniques such as dropout were implemented⁷². The NLL loss for a single data point is given by

where y is the true class label and \({\hat{y}}_{y}\) is the predicted probability for the true class label y.

The loss for a batch of data is the mean of the individual losses for each data point in the batch:

where N is the number of data points in the batch, y_i is the true class label for the ith data point and \({\hat{y}}_{{y}_{i}}\) is the predicted probability for the true class label of the ith data point.

In the hyperparameter tuning process, we used Optuna, an optimization framework, to adjust parameters such as the number of hidden dimensions, embedding dimensions and layers within the model. The model presented in this research integrated a deep learning architecture. This architecture was designed to incorporate prior information (samples) into the generative process. Additionally, the model used Chemistry42 feedback in conjunction with QCBMs, aimed at enhancing its generative accuracy. Supplementary Figure 4 illustrates the proposed architecture at a cell level. The prior samples were combined with input samples \(x^{\prime}_t = X(i) +\!\!\!\!+ x_t\) in the LSTM cell. This combination constituted two methods: adding and concatenating samples. The LSTM’s operations were updated with the following operations:

To generate samples, the process began with sampling from the prior, followed by the LSTM network processing these prior samples to generate compounds representations. The compounds were validated through the Chemistry42 platform, specifically tailored to assess ligand quality for the KRAS-G12D mutant. This methodology allows designing ligands targeted at specific proteins. Moreover, the LSTM model is a classical approach for learning ligand structures and constructing a latent ligand space. The QCBM functions as a prior, guiding the LSTM in the generation of novel ligand samples. The procedure was subjected to an iterative process to enhance the quality of ligands, which was evaluated using the Chemistry42 platform.

Quantum generative model: QCBM model

The QCBM is a variational quantum algorithm that uses the foundational principles of quantum mechanics, particularly the Born rule, to generate complex and diverse data samples. The core of our QCBM model is a parameterized quantum state \(\left\vert \psi (\theta )\right\rangle\), where θ denotes the parameters or ansatz of our quantum circuit. As per the Born rule, given a measurement basis, which is commonly the computational basis in our case, the probability of observing a specific outcome \(\left\vert x\right\rangle\) is expressed as ∣〈x∣ψ(θ)〉∣².

Training a QCBM involves optimizing the parameters of the quantum circuit to produce a probability distribution that closely approximates the target distribution (probability computed by Chemistry42 reward values). This process is fundamentally iterative, where the quantum circuit parameters, denoted as θ, are adjusted in each step to reduce the discrepancy between the generated and target distributions. A classical optimization algorithm recommends adjusting parameters, which operates on the basis of the feedback received from the evaluation of the circuit’s output. At each iteration, the quantum circuit is sampled to produce a set of states. These states are then compared against the target distribution and the difference between them informs the direction and magnitude of parameter adjustments in the quantum circuit. This iterative process continues until the distribution generated by the QCBM closely aligns with the target distribution or until a predefined convergence criterion is met.

In the context of QCBM training, the exact NLL functions as the primary loss function, providing a quantitative measure of the difference between the distributions. The exact NLL for a QCBM is the negative sum of the logarithms of the probabilities that the quantum circuit assigns to the states in the training dataset. Mathematically, this is represented as \(\,\text{NLL}\,(\theta )=-{\sum }_{x\in D}\log {p}_{\theta }(x)\), where D is the set of data points and p_θ(x) is the probability of observing state x under the current parameters θ of the quantum circuit. Minimizing the NLL involves adjusting θ such that the quantum circuit’s output distribution increasingly resembles the empirical distribution of the data. This optimization is typically carried out using gradient-based methods or other heuristic techniques suited to the quantum computing context. In our project, we used COBYLA for our optimizer. As the NLL decreases, the fidelity of the QCBM in modeling the target distribution correspondingly increases, indicating successful training of the quantum model.

Extended Data Fig. 5 shows the QCBM architecture and illustrates its associated ansatz. We used linear topology for our project. Our QCBM model was built with 16 qubits and four layers and we had 96 parameters to optimize in total. The initial probability of the samples, P(X(i)), was computed on the basis of the rewards returned by the Chemistry42 model. These reward-based probabilities were then passed through a softmax function to ensure that they were normalized and fell within the range of 0–1. The resulting values served as the ‘true’ probabilities of the samples and were used as the target values during the model’s training process.

Algorithm 2

Algorithm 2 provides the pseudocode outlining the training regimen for the QCBM model. This process delineates the iterative optimization of the QCBM parameters.

1: Initialize: QCBM model with a certain number of qubits and layers

2: Set: Parameterized quantum state \(\left\vert \psi (\theta )\right\rangle\)

3: while not converged do

4:  Compute exact NLL loss function

5:  Compute gradient of exact NLL with respect to θ

6:  Adjust parameters using an optimizer

7:  Validate the sample and compute its reward value

8:  if sample is valid then

9:    Compute rewards for the sample

10:    Adjust probabilities P(X_i) on the basis of the rewards

11:    Train QCBM model with adjusted probabilities

12:  end If

13: end while

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.