A neural network for long-term super-resolution imaging of live cells with reliable confidence quantification

Optical setup and data acquisition

The Multi-SIM system was built on the basis of an invented fluorescence microscope (Ti2E, Nikon). Briefly, three laser beams of 488 nm (Genesis-MXSLM, Coherent), 560 nm (2RU-VFL-P-500-560, MPB Communications) and 640 nm (LBX-640-500, Oxxius) were combined collinearly and then passed through an acousto-optic tunable filter (AOTF, AOTFnC400.650, AA Quanta Tech). Afterward, the selected laser light was expanded and sent into an illumination modulator, which was composed of a ferroelectric spatial light modulator (SLM, QXGA-3DM, Forth Dimension Display), a polarization beam splitter and an achromatic half-wave plate. Different illumination modes were generated by adjusting the patterns displayed on the SLM, for example, grating patterns of 3 phases × 3 orientations at 1.41 numerical aperture (NA) for TIRF-SIM or 1.35 NA for GI-SIM. Next, the modulated light was passed through a polarization rotator consisting of a liquid crystal cell (Meadowlark, LRC-200) and a quarter-wave plate, which rotated the linear polarization to maintain the necessary S-polarization, thus maximizing the pattern contrast for all pattern orientations. The diffraction orders, except for ±1 orders for TIRF/GI-SIM, were filtered out by a spatial mask and then relayed onto the back focal plane of the objectives (1.49 NA, Nikon). The raw SIM images excited by different illumination patterns were sequentially collected by the same objective, then separated by a dichroic beam splitter (Chroma, ZT405/488/560/ 647tpc) and finally captured with an scientific complementary metal–oxide–semiconductor camera (Hamamatsu, Orca Flash 4.0 v3). We separately optimized the illumination pattern for each color channel and SIM reconstruction algorithm according to the objective NA and corresponding excitation wavelength, resulting in superior imaging quality for all channels in multicolor imaging. The Multi-SIM system integrates diverse imaging modes (TIRF/GI, TIRF/GI-SIM, three-dimensional (3D)-SIM, stacked slice-SIM, etc.) into a single setup, which is commercially available from NanoInsights.

In the BioTISR dataset, for each type of specimen and each imaging modality, we acquired the raw data from at least 50 distinct regions of interest (ROIs). For each ROI, we acquired 2–4 groups of raw images with N phases × M orientations × T time points with a constant exposure time but escalating excitation light intensity, where (N, M, T) corresponded to (3, 3, 20) for TIRF-SIM and GI-SIM, (5, 5, 10) for nonlinear SIM and (3, 5, 10) for 3D-SIM. Each set of N × M × T raw images were averaged as diffraction-limited time-lapse WF images or stacks, which were then used as the input LR image for TISR networks. Meanwhile, the raw images acquired with the highest excitation power were reconstructed into GT-SIM images or stacks, which served as the targets in model training. For better clarity, we summarize the imaging conditions and detailed information of the BioTISR dataset in Supplementary Table 1.

In long-term live-cell imaging experiments, cells were held in a stage-top incubator equipped on the microscope (OkO Lab, H301) to maintain conditions at 37 °C with 5% CO₂. We used the TIRF/GI mode and GI-SIM mode to acquire the WF or raw SIM images (which could be reconstructed into conventional SR-SIM images for comparison) and then obtained SR images using the DPA-TISR or Bayesian DPA-TISR models. The detailed imaging conditions of live-cell imaging experiments are summarized in Supplementary Table 2.

Network configurations for TISR model evaluation

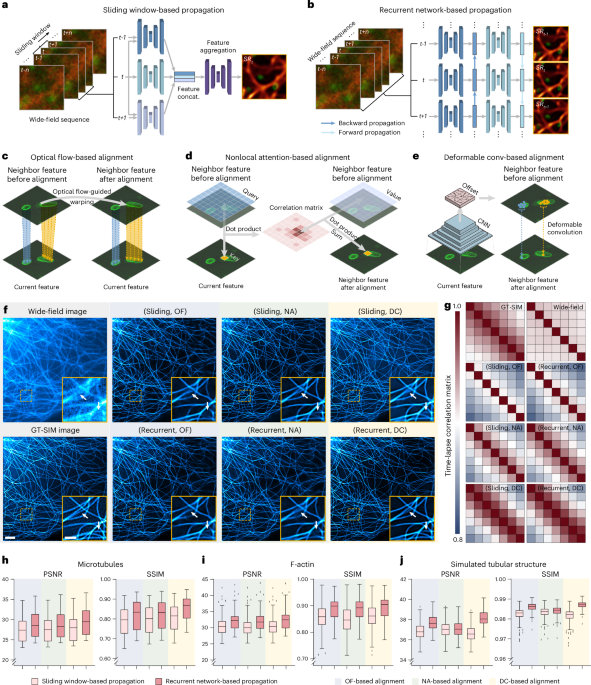
For fair comparison, we designed a template TISR model with the propagation and alignment modules replaceable, as depicted in Extended Data Fig. 2. The template TISR model was modified from the foundational BasicVSR++ neural network²¹. It comprises three primary modules: a feature extraction module, a propagation and alignment module and a reconstruction module. This architecture is meticulously crafted to be compatible with distinct components of the computational process. For a given image sequence X = {x_i−k, x_i−k+1, …, x_i, …, x_i+k−1, x_i+k}, three identical residual blocks are used to extract features from each frame. Each residual block comprises two convolutional layers, a leaky rectified linear unit activation function and a skip connection. Before passing through the residual blocks, a convolutional layer is applied for channel augmentation. The operation of feature extraction module can be formulated as

where f(∙) is a convolutional layer and RB is a residual block.

Subsequently, the output feature maps are fed into the propagation and alignment module through two distinct schemes, referred to as SWP and RNP.

In the SWP scheme, feature maps from the central and adjacent frames within a local window are severally fed into an alignment block to refine all neighbor features towards the central frame. The alignment block consists of an alignment module, a convolutional layer and three residual blocks. In our validation, three distinct alignment modules based on OF, DC and NA are used (Extended Data Fig. 2c–e). Afterward, the resulting feature maps are concatenated and go through a 1 × 1 convolutional layer to reduce the channels. The progress of SWP can be articulated as follows:

where \(\oplus\) denotes channel-wise concatenation and AB is an alignment block.

In the RNP scheme, the feature maps from adjacent frames generated by the feature extraction module propagate forward and backward in the time dimension following the second-order grid propagation manner²¹. Given the feature map \({x}_{i}^{1}\) and corresponding features propagated from the first-order neighborhood (h_i+1,h_i−1) and second-order neighborhood (h_i+2,h_i−2), we have

where \({g}_{i}^{\,\rm{backward}}\) and \({g}_{i}^{\rm{forward}}\) represent the feature computed at the ith timestep in backward and forward propagation, respectively.

In the OF-based alignment block, we compute the OF between neighbor frames using SPyNet⁴⁶. If we denote the OF from \({x}_{i-k}\) to x_i as \({f}_{i-k\to i}\), the neighbor features \({h}_{i-k}\) will be aligned according to \({x}_{i}\) by directly warping using the OF computed from \({x}_{i-k}\) and x_i:

where W denotes the spatial warping operation.

In DC-based alignment block, the OF \({f}_{i-k\to i}\) is used to prealign the features. The aligned features are then concatenated with the current features \({x}_{i}^{1}\) and OF \({f}_{i-k\to i}\) to compute the DC offset \({o}_{i-k\to i}\) and modulation mask \({m}_{i-k\to i}\) with two sequential residual blocks:

where σ denotes the sigmoid activation function. A DC layer is then applied to the unwrapped feature \({h}_{i-k}\):

where D denotes a DC.

In NA-based alignment block, three fully connected layers are initially used to generate the embedded query, key and value:

where F denotes a fully connected layer. Then, the NA mechanism is applied for feature alignment:

where \({\rm{\otimes }}\) refers to dot product operation. In practice, the embedded features have half of the channels compared to the original feature and we adopt a neighborhood attention mechanism⁴⁷, which can be regarded as a more efficient implementation of NA in our experiments, achieving similar SR performance.

Lastly, the aligned hierarchical features undergo through the reconstruction module consisting of three residual blocks, a pixel shuffle layer and a concluding convolutional layer to generate the SR residuals, which are then added up with upsampled raw input images, yielding final TISR images. The operation of the reconstruction module can be formulated as follows:

Taking the final output of RM as \({\hat{y}}_{i}\) and the GT as y_i for the ith frame, the overall objective function can be formulated as

The trainable parameter numbers of TISR models constructed as described are listed as follows: 5.58 million (sliding, OF), 5.59 million (sliding, NA), 7.97 million (sliding, DC), 3.95 million (recurrent, OF), 3.71 million (recurrent, NA) and 5.40 million (recurrent, DC).

Network architecture of DPA-TISR

DPA-TISR was constructed on the basis of the optimal TISR baseline model (that is, adopting recurrent network for propagation and DC for alignment), following the evaluation conclusions in Fig. 1. In DPA, as depicted in Fig. 2a and Extended Data Fig. 4b, the phase-space alignment mechanism serves as a complementary module to spatial DC, synergistically improving the alignment between neighborhood feature maps \({h}_{i-k}\) and current feature maps h_i. Specifically, the DPA begins with the real-valued fast Fourier transform (denoted as FFT(∙), implemented with torch.fft.rfft) to extract the amplitude and phase of both \({h}_{i-k}\) and h_i:

where \({\rm{Angle}}(\bullet )\) and \({\rm{Abs}}(\bullet )\) represent the operation to obtain the element-wise angle and absolute value of the features. Then. the concatenation of phases from current and neighborhood feature maps further goes through a phase-space convolution module, containing one convolutional layer followed by two residual blocks and a skip connection:

An inverse real-valued FFT (denoted as iFFT(∙), implemented with torch.fft.irfft) is then used to reconstruct the space-domain feature maps from the obtained amplitude and phase components:

The phase-refined feature maps are then fed into the DC module as depicted in Extended Data Fig. 2 for subsequent spatial alignment. The overall architecture of DPA-TISR is illustrated in Extended Data Fig. 4.

To adapt DPA-TISR to SIM reconstruction and volumetric SR inference, we further modified it into DPA-TISR-SIM and 3D DPA-TISR, respectively. The primary modifications are depicted in Supplementary Fig. 12 and described in detail in Supplementary Note 5.

Assessment metric calculation

We performed image normalization for GT-SIM and TISR images following a commonly used procedure^5,11. Specifically, each GT-SIM image stack Y was normalized by dividing by the maximum value, then blurred by a 3 × 3 size Gaussian kernel with the s.d. = 0.4 (denoted as ρ(∙)) to mitigate the SIM reconstruction artifacts:

Before computing the assessment metrics (that is, PSNR and SSIM), a linear transformation was applied to each SR image stack H:

where \({\rm{\alpha }}\) and \({\rm{\beta }}\) were chosen by solving the convex optimization problem:

where \({{||}\bullet {||}}_{2}\) denotes L₂ normalization. The optimized \(\alpha\) and \(\beta\) result in an MSE-minimized linear transformation of \({{H}}\), effectively scaling and translating every pixel to match the dynamic range of the GT.

Three types of metrics were used for quantitatively evaluating the performance in output fidelity, resolution and temporal consistency. PSNR and SSIM were used to evaluate pixel-level similarity between the inferred SR images and GT-SIM images. Decorrelation analysis⁴⁸ was applied to quantify the image resolution. For temporal consistency assessment, a time-lapse Pearson’s correlation matrix was used to visualize the similarity between adjacent SR images \({\{{H}_{i}\}}_{i=1}^{n}\). The Pearson correlation between images x and y is calculated by

where μ and σ denote the mean value and s.d. of corresponding images, respectively, and E represents the arithmetic mean.

Comparison of DPA-TISR with other models

For the comparative analysis between TISR and SISR models in Figs. 2 and 4 and Extended Data Fig. 7, we modified the 3D DPA-TISR into its SISR counterpart by excluding all operations related to alignment and propagation while keeping other network components (that is, the feature extraction module, reconstruction module and residual blocks in the alignment module), identical to (3D) DPA-TISR. As such, the temporal feature aggregation capability of 3D DPA-TISR was dismissed, yielding a pure SISR manner. Considering that the above SISR modification may cause a reduction in trainable parameters (for example, ~7 million for DPA-TISR versus ~5.5 million for SISR), we further compared DPA-TISR to its SISR counterparts with parameter compensation by adding additional residual blocks into SISR models (Supplementary Fig. 18), which verifies that the superiority of DPA-TISR over SISR mainly comes from the use of temporal information, rather than gain of trainable parameters.

In the comparative analysis between DPA-TISR and other TISR models (that is, VRT and BasicVSR++), we used their publicly available implementations on GitHub^21,27. All networks were trained with the same dataset and configurations (initial learning rate, learning rate decay, batch size, etc.) for fair comparison. It is noteworthy that the patch size of VRT was adjusted to 64, half that for other models, to ensure similar graphics processing unit (GPU) memory usage.

Implementation details of TISR models

The implementation procedure of TISR model typically includes three steps: training data preparation, model training and model inference. In this work, all TISR models were trained using the BioTISR dataset (Supplementary Table 1) unless otherwise stated. As described above, there are over 50 groups of paired WF–GT sequences for each biological specimen. Typically, we selected 40 of these groups for training and validation and used the remaining ~10 groups for testing. Before training, each group of data was augmented into time-lapse image pairs with the size of 128 × 128 × 7 for WF input and 256 × 256 × 7 or 384 × 384 × 7 for corresponding GT-SIM images by random cropping, horizontal or vertical flipping and random rotation for further enrichment and avoiding overfitting. In particular, we conducted an evaluation on DPA-TISR models trained with different lengths of input sequence and found that the input length of 7 was optimal to balance the computation efficiency and SR performance (Supplementary Fig. 19). In the live-cell experiments, we independently trained a specified DPA-TISR model for each type of biological structures (that is, each color channel) for best SR performance.

The training and inference were performed on a computer workstation equipped with four GeForce RTX 3090 graphic processing cards (NVIDIA) with Python 3.6 and PyTorch 1.12.1. In the model training procedure, the batch size for all experiments was set to 3 and all models were trained using the Adam optimizer with an initial learning rate of \(5\times {10}^{-5}\), which was decayed by 0.5 for every 1,000 epochs. The training process typically took 18 h within approximately 3,000 epochs. Once the networks were trained, TISR models could be applied to process other images of the same specimen, typically taking about 1 s to reconstruct a seven-frame SR stack of 1,024 × 1,024 pixels. The time required for both training and inference decreases linearly with the increase in the number of GPUs used and multi-GPU acceleration has been incorporated into our publicly available Python codes. Detailed instructions about environment installation, inference with pretrained model, training new models, confidence correction fine-tuning, etc. can be found in the GitHub repository of Bayesian DPA-TISR (https://github.com/liushuran2/Bayesian_DPA_TISR).

Calculation of uncertainty

The reliability of DPA-TISR predictions can be quantified through two types of uncertainties: model uncertainty and data uncertainty, also referred to as epistemic uncertainty and aleatoric uncertainty, respectively, in Bayesian analysis¹⁶.

Considering the non-Bayesian DPA-TISR, represented by \({f}_{\theta }\), where \(\theta\) indicates the trainable parameters, the output SR image sequence is denoted as \(\hat{{\rm{y}}}={f}_{\theta }(x)\). The network parameters are chosen by minimizing the pixel-wise distance between GT y and \(\hat{{\rm{y}}}\). Taking the L₁ loss as an example, the objective function can be expressed as follows:

where T denotes the number of time points and N denotes the number of pixels in a single image.

Inspired by previous work^11,17, we designed the Bayesian DPA-TISR that predicts both the intensity \({\hat{y}}_{n}\) and the scale \({\hat{\sigma }}_{n}\) for every pixel. Instead of considering each pixel as a single intensity value, we modeled it as a Laplace distribution empirically:

In this way, the scale \(\hat{\sigma }\) can be regarded as a measurement of the data uncertainty. Then, the output SR image \(\hat{y}\) and the scale \(\hat{\sigma }\) can be simultaneously addressed by minimizing the negative log-likelihood (NLL) function:

To characterize the model uncertainty, we adopted a Bayesian approximation approach¹⁷ that uses a distribution over model parameters by incorporating concrete dropout after convolutional layers. Within each inference, the dropout layers in Bayesian DPA-TISR randomly zeroized half of the neurons, thus yielding a distinctive model. Then, by aggregating a certain number (denoted as M) of the outcomes of the stochastic forward propagation, the SR results of Bayesian DPA-TISR can be obtained by averaging the predicted intensity of each trial:

where \({\hat{{{y}}}}^{(m)}\) is the predicted intensity map from the \({m}{\rm{th}}\) network. The model uncertainty is then quantified by calculating the standard deviation of the predicted results:

Subsequently, the overall data uncertainty is assessed as follows:

where \({\hat{\sigma }}^{(m)}\) is the predicted scale map from the \({m}{\rm{th}}\) network.

Calculation of confidence map

To enhance the integration of model and data uncertainty information and provide biologists with a more intuitive measurement of uncertainty, we take one step further by using a pixel-wise mixture probability distribution to generate an integrated confidence map.

During the inference stage, we independently generated M models \({\theta }^{(m)}\), differing only through dropout layers as depicted above. Considering inferences from M independent models, each pixel \(i\) follows a mixed Laplace distribution (example in Fig. 4a):

where \(\varOmega ={\{{\theta }^{(m)}\}}_{m=1}^{M}\) and \({x}_{p}\) is the coordinate of the PDF.

Accordingly, we defined the credible interval \({A}^{\varepsilon }=[{\hat{y}}_{\rm{mean}}-\varepsilon ,{\hat{y}}_{\rm{mean}}+\varepsilon ]\) and the interval length ε. Then, the corresponding confidence p^ε,i for pixel \(i\) is defined as the probability that the true value y falls within A^ε:

After defining a proper value for \({{\varepsilon }}\) (Supplementary Note 7), which was empirically set to 0.04 by default in our experiments, a confidence map can be generated to indicate the probability that the true value falls within the predicted credible interval.

Implementation details of Bayesian DPA-TISR

On the basis of the uncertainty and confidence calculation mentioned above, we designed Bayesian DPA-TISR, which differs from DPA-TISR in three main aspects. First, we integrated a dropout layer after each convolutional layer in the feature extraction module and reconstruction module, randomly deactivating neurons during both training and prediction stages. Notably, we did not apply dropout in the propagation and alignment module as we empirically found that any dropout here resulted in noticeable SR performance decline speculatively because of the temporal information loss during propagation and alignment (Supplementary Fig. 14b), while appropriate dropout (that is, with dropout rate lower than 0.5) in the feature extraction module and reconstruction module slightly benefited the overall SR performance (Supplementary Fig. 14c). Second, we adjusted the output channel number of the last convolutional layer in DPA-TISR from one to two, representing the predicted mean and scale, respectively. An additional sigmoid function was applied to the predicted scale channel to ensure its non-negativity. Third, the objective function was modified from L₁ loss to NLL loss as formulated in equation (24).

During inference stage, we independently executed the trained network with dropout six times (that is, M = 6), averaged the results as the final SR output and generated a confidence map as described previously. In particular, in long-term confidence-quantifiable TISR imaging experiments, we observed that the predicted scales tended to increase with the corresponding inferred intensities, making it unintuitive to discern which area of an output image is reliable or unreliable solely from the confidence map. To address this issue, we adopted an intensity-aware confidence generation scheme. Instead of using a constant \(\varepsilon\) of the credible interval \({A}^{\varepsilon }=[\,\hat{{{y}}}-\varepsilon ,\hat{{{y}}}+\varepsilon ]\) (hereafter, \({\hat{y}}_{\rm{mean}}\) is denoted by \(\hat{y}\) for simplicity), we modified the interval length \(\varepsilon\) as follows:

where the scalar scaling factor γ and ε were empirically set to 0.2 and 0.04, respectively, in our experiments. Using \(\bar{\varepsilon }\) essentially defines a threshold of 0.2 for foreground segmentation. For pixels with values greater than 0.2, which are more likely to belong to the actual structure, we assigned a proportion (0.2) of their absolute intensity as the interval length. Conversely, for pixels with values less than 0.2, typically representing the background region, we assigned a constant value of 0.04 as the interval length, thereby rationalizing the confidence calculation within background regions of the inferred TISR image.

Calculation of ECE and reliability diagram

To evaluate the effectiveness of the uncertainty and confidence map, the reliability diagram that compares the empirical accuracy to averaged confidence was computed following a standard procedure¹¹ in our experiments. Well-calibrated confidence in the reliability diagram should yield confidence values similar to accuracy, resulting in a diagonal diagram.

Specifically, the empirical accuracy is defined as the proportionality that the GT \(y\) falls into the credible interval \({A}^{\varepsilon }=[\,\hat{{{y}}}-\varepsilon ,\hat{{{y}}}+\varepsilon ]\). Consequently, the accuracy and confidence are specified as follows:

where \({{S}}\) denotes a subset of all pixels, 1(∙) denotes the indicator function and ε > 0 determines the length of the credible interval around each \(\hat{{{y}}}\).

To construct a reliability diagram with K groups, we divided the value of confidence into K intervals segmented by τ₀, τ₁, …, τ_K. For pixels in \({S}_{k}^{\varepsilon }=\{{p}^{\varepsilon }\epsilon ({\tau }_{k-1},{\tau }_{k}]\}\), we plotted \({\rm{Confidence}}(\,{{\hat{y}},{\hat{f}}\,{|}S}_{k}^{\varepsilon },{{\varepsilon }})\) against \({\rm{Accuracy}}(\,{{\hat{y}},{y\; |}S}_{k}^{\varepsilon },{{\varepsilon }})\) to obtain the final reliability diagram. Furthermore, the ECE was determined as the weighted average of the absolute differences between the accuracy and confidence:

Confidence correction for Bayesian DPA-TISR

Recognizing the disparity between the estimated confidence and actual accuracy (that is, overconfidence for most Bayesian neural networks), we developed an iterative fine-tuning framework to eliminate the ECE between the estimated confidence and accuracy. During the fine-tuning stage, the objective function was modified from equation (24) as follows:

where \({R}_{\rm{confidence}}\) is the CCR and \(\alpha\) is a weighting scalar to balance \({{\mathscr{L}}}_{{NLL}}\) and \({R}_{\rm{confidence}}\), which was empirically set to 0.1 in our experiments. CCR comprises two parts:

where the second term, \({\rm{confidence}}\left({\hat{y}},{\hat{f}}\,|{{\varepsilon }}\right)\), is the average confidence of the outputs and the corresponding weighting scalar \(k\) aims at adjusting overall average confidence of prediction. Positive values of k suppress overconfidence and negative values of k restrain underconfidence, which is the key variable in our optimization framework. We adopted a combined strategy of linear searching and parabola fitting to determine the optimal value of k.

In the optimization process, a relative ECE (rECE) of the original trained network, denoted as E₀, is first calculated by

of which the sign is used to determine the initial direction for subsequent optimization:

where \({\Delta}\) is the step size set to 0.1 by default. Next, the first two trials of fine-tuning are independently performed with \({k}_{1}\) and \({k}_{2}\), respectively, using the objective function described in equation (34), after which we obtain two new ECE values of the fine-tuned networks, denoted as \({E}_{1}\) and \({E}_{2}\). If \({E}_{1} < {E}_{2}\), we exchange \({k}_{1}\) and \({k}_{2}\), as well as the corresponding \({E}_{1}\) and \({E}_{2}\), and reverse the searching direction (that is, reset \({\Delta}\) as −0.1) to ensure that \({k}_{2}\) is the ECE-descent direction compared to \({k}_{1}\). Afterward, the linear searching process continues along this descent direction,

until finding a \({k}_{i}\) value that satisfies \({E}_{i} > {E}_{i-1}\), where \({E}_{i}\) denotes the ECE value of the fine-tuned model with \({k}_{i}\). We then use the quadratic polynomial fitting to find the optimal \({k}_{* }\) value according to the three latest weighting scalars \({k}_{i},\,{k}_{i-1},\,{k}_{i-2}\) and corresponding ECE values \({E}_{i},{{E}}_{i-1},\,{E}_{i-2}\):

One final fine-tuning is carried out using the optimal \({k}_{* }\) in the objective function to obtain a confidence-calibrated Bayesian DPA-TISR model. During the fine-tuning stage, the model was trained using the Adam optimizer with an initial learning rate of \(5\times {10}^{-5}\), which is decayed following a cosine annealing strategy over a course of 30 epochs. The overall fine-tuning process typically takes less than 1 h. The workflow diagram of the confidence correction is shown in Supplementary Fig. 20.

Mito–PO contact quantification

The contact level between Mito and POs was evaluated by confidence-weighted MOC. Considering that Mito–PO contact sites were principally situated at the periphery of POs, we first identified the boundary of each PO using the following procedure: (1) the background of the ROI of the PO was estimated by applying a Gaussian filter with s.d. = 10 pixels; (2) the TISR image was smoothed using another Gaussian filter with s.d. = 1 pixel and then the estimated background was subtracted; (3) a binary mask was generated by setting a threshold to the background-subtracted image; (4) the boundary of each PO was extracted using the Sobel operator; and (5) the PO boundary image was convolved with the equivalent PSF of SIM, thereby delineating potential contact regions of POs. Next, following steps 1–3, a binary Mito mask, denoted as \({{{M}}}_{{\rm{Mito}}}\), was calculated.

We reasoned that the regions with higher confidence should have higher weights in MOC calculation. Therefore, we applied the confidence map estimated by the Bayesian DPA-TISR model as adaptive wights to rationalize the quantification of Mito–PO contacts as follows:

where \({{{Y}}}_{{{i}}}\), \({{{M}}}_{{\rm{Mito}},{{i}}}\) and \({{{C}}}_{{\rm{Mito}},{{i}}}\) denote the value of the \({i}{\rm{th}}\) pixel in the ROIs of the PO boundary image \({{Y}}\), Mito mask \({{{M}}}_{{\rm{Mito}}}\) and the confidence map \({{{C}}}_{{\rm{Mito}}}\).

Cell culture, transfection and staining

COS-7 and HeLa cells, as well as their stable cell lines, were cultured in DMEM (Gibco, 11965092), supplemented with 10% FBS (Gibco, 10099141C) and 1× penicillin–streptomycin (Thermo Fisher Scientific, 15140122) at 37 °C in a Thermo Fisher Scientific Heracell 150i CO₂ incubator. SUM159 cells were cultured in DMEM/F12K medium supplementary with 5% FBS and 1% penicillin–streptomycin solution.

For live-cell imaging, the 35-mm coverslips were precoated with 50 μg ml⁻¹ collagen and 1 × 10⁵ cells were seeded onto coverslips. For transient transfection, cells were transfected with plasmids using Lipofectamine 3000 (Invitrogen, L3000150) according to the manufacturer’s protocol 12 h after plating. Cells were imaged for 12 h after transfection. Where indicated, the cells transfected with Halo-tagged plasmids were labeled with 10 nM JF549 ligand for 15 min according to the published protocol⁴⁹. The cells were rinsed with fresh medium to remove unbound ligand and imaged immediately afterward. The plasmids used in transient transfection included Lifeact–mEmerald, Lifeact–SkylanNS, Clathrin–mEmerald, Clathrin–mCherry, 3×mEmerald–Ensconsin, Lamp1–Halo, 2×mEmerald–Tomm20, TFAM–mEmerald, PKMO–Halo and PMP–Halo.

Statistics and reproducibility

Figures 1h–j and 2e,f and Extended Data Figs. 3c,d, 5f,h, 6c,d and 7e were plotted in Tukey box-and-whisker format. The box extends from the 25th and 75th percentiles and the line in the middle of the box indicates the median. The upper whisker represents the larger value between the largest data point and the 75th percentile plus 1.5× the interquartile range (IQR) and the lower whisker represents the smaller value between the smallest data point and the 25th percentile minus 1.5× the IQR. Data points larger than the upper whisker or smaller than the lower whisker were identified as outliers and are displayed as black spots.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.